softmax¶

In [1]:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

%matplotlib inline

In [2]:

def indentify(x):
    return x

In [21]:

# http://stackoverflow.com/questions/3985619/how-to-calculate-a-logistic-sigmoid-function-in-python
from scipy import stats
from scipy import special

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

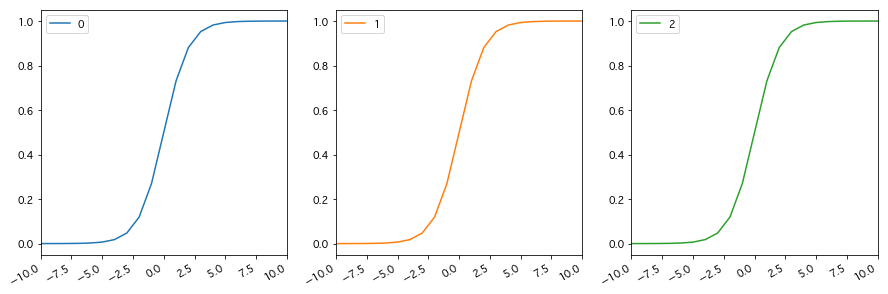
pd.concat([
    pd.Series(np.arange(-10,11), index=range(-10,11)).apply(sigmoid),
    pd.Series(range(-10, 11), index=range(-10,11)).apply(stats.logistic.cdf),
    pd.Series(range(-10, 11), index=range(-10,11)).apply(special.expit),
], axis=1).plot(subplots=True, layout=(1,3), figsize=(15,5))

Out[21]:

array([[<matplotlib.axes._subplots.AxesSubplot object at 0x1130ac5f8>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x112392518>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x112349cc0>]], dtype=object)

../../../_images/contents_notebooks_scratch_softmax_3_1.png

In [30]:

# http://stackoverflow.com/questions/34968722/softmax-function-python
def softmax(x):
    return np.exp(x) / np.exp(x).sum()

In [29]:

x = np.array(list(range(-2, 3)))
softmax(x), sum(softmax(x))

Out[29]:

(array([ 0.01165623,  0.03168492,  0.08612854,  0.23412166,  0.63640865]), 1.0)

In [31]:

# http://stackoverflow.com/questions/3985619/how-to-calculate-a-logistic-sigmoid-function-in-python
# http://hamukazu.com/2015/07/31/mathematical-derivation-in-numerical-computation/