Standardize_other

  • 1 pandas notes
  • 2 環境準備
  • 3 データ準備のための準備
  • 3.1 [0, 1)
  • 4 正規分布？
  • 4.1 カテゴリ変数化
  • 5 quantile
  • 6 基礎集計
  • 7 正規化
  • 8 累積構成比のための処理
  • 9 分布
  • 10 formula式

pandas notes

  • pandasのメモ
  • python3.5.1を使うようにする
  • pandas 0.17.1を使うようにする

環境準備

pyenv install anaconda3-2.5.0
pyenv local anaconda3-2.5.0

In [50]:

import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
plt.style.use('ggplot')

%matplotlib inline

データ準備のための準備

In [25]:

nrow, ncol = 2, 3

[0, 1)

In [26]:

np.random.rand(nrow, ncol)

Out[26]:

array([[ 0.90160673,  0.50850989,  0.60819238],
       [ 0.03801823,  0.12838991,  0.05579081]])

正規分布？

In [27]:

np.random.randn(row_count, col_count)

Out[27]:

array([[-0.41047876,  0.96353492, -0.52898658],
       [ 1.17824705, -0.44607617, -0.25503468]])

In [71]:

pd.Series(np.random.randn(1, 10000)[0], name="a").hist()

Out[71]:

<matplotlib.axes._subplots.AxesSubplot at 0x11c6e3a20>
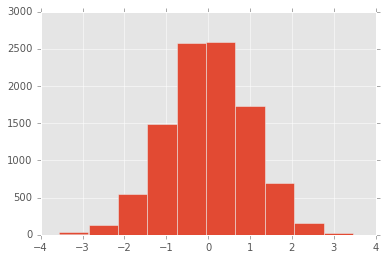
../../../_images/contents_notebooks_pandas_Standardize_other_9_1.png 
In [64]:

np.random.randn(1, 10000)

Out[64]:

array([[ 1.01418904, -0.38533656,  2.02055062, ...,  1.58338601,
        -1.42410101,  0.16196371]])

In [28]:

np.random.randint(1, 100, 10)

Out[28]:

array([ 8, 52, 30, 40, 42, 21, 34, 11, 77, 48])

In [80]:

import string

np.random.seed(0)
data = {
    "a": range(1, 1000+1),
    "b": list(string.ascii_letters[:25] * 40),
    "c": [1,2,3,4] * 250,
    "d": np.random.rand(1000),
    "e": np.random.randn(1000),
    "f": np.random.randint(1, 100, 1000)
}
df = pd.DataFrame(data)
df.head(5)

Out[80]:
a b c d e f
0 1 a 1 0.548814 -0.101697 53
1 2 b 2 0.715189 0.019279 76
2 3 c 3 0.602763 1.849591 54
3 4 d 4 0.544883 -0.214167 94
4 5 e 1 0.423655 -0.499017 68 
In [81]:

df["c"].head(1)

Out[81]:

0    1
Name: c, dtype: int64

カテゴリ変数化

In [82]:

df["c"] = df.c.astype("category")
df["c"].head(1)

Out[82]:

0    1
Name: c, dtype: category
Categories (4, int64): [1, 2, 3, 4]

quantile

In [32]:

df.quantile()

Out[32]:

a    500.500000
d      0.481323
e      0.030935
f     51.000000
dtype: float64

In [33]:

decile = list(map(lambda x: x / 10, range(0, 10+1)))
decile

Out[33]:

[0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]

In [34]:

deciled = df.quantile(decile)
deciled

Out[34]:
a d e f
0.0 1.0 0.000546 -2.994613 1
0.1 100.9 0.100287 -1.198404 9
0.2 200.8 0.203938 -0.825520 22
0.3 300.7 0.292981 -0.481149 33
0.4 400.6 0.383455 -0.199363 41
0.5 500.5 0.481323 0.030935 51
0.6 600.4 0.588486 0.245125 60
0.7 700.3 0.696379 0.501393 69
0.8 800.2 0.806419 0.835011 79
0.9 900.1 0.907747 1.324424 89
1.0 1000.0 0.999809 3.170975 99

基礎集計

  • 平均値
  • 中央値
  • plot moduleを試した
In [35]:

mean = pd.DataFrame(df.mean()).T
mean

Out[35]:
a d e f
0 500.5 0.495922 0.029044 50.372 
In [36]:

median = pd.DataFrame(df.median()).T
median

Out[36]:
a d e f
0 500.5 0.481323 0.030935 51 
In [37]:

df["d"].plot(kind="hist", bins=20)

Out[37]:

<matplotlib.axes._subplots.AxesSubplot at 0x11b603c18>
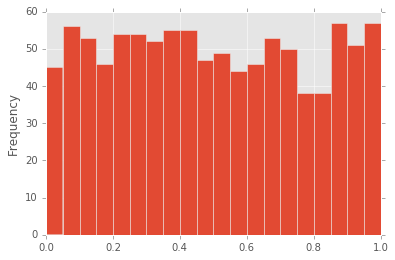
../../../_images/contents_notebooks_pandas_Standardize_other_23_1.png 
In [38]:

df["d"].plot.hist(bins=20)

Out[38]:

<matplotlib.axes._subplots.AxesSubplot at 0x11b788748>
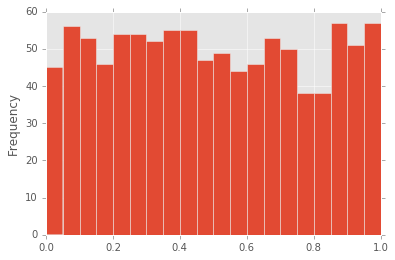
../../../_images/contents_notebooks_pandas_Standardize_other_24_1.png

正規化

In [114]:

from sklearn.preprocessing import scale
# normalize はベクトルの正規化だった
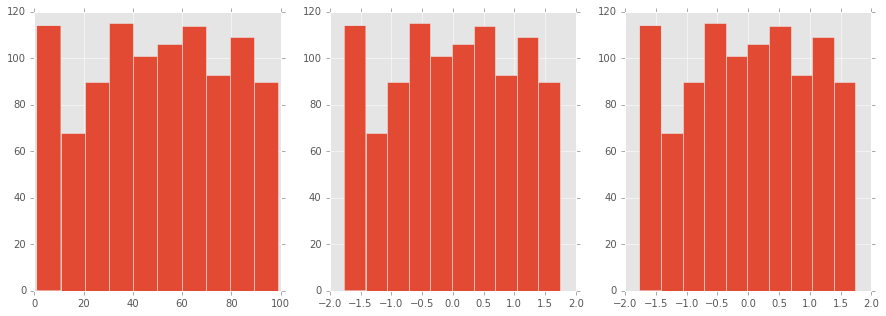
figure, axes = plt.subplots(1, 3, figsize=(15, 5))
df["f"].hist(ax=axes[0])
(df.f - df.f.mean()).div(df.f.std()).hist(ax=axes[1])
plt.hist(scale(df["f"].astype("float")))

Out[114]:

(array([ 114.,   68.,   90.,  115.,  101.,  106.,  114.,   93.,  109.,   90.]),
 array([-1.76395676, -1.41382356, -1.06369036, -0.71355717, -0.36342397,
        -0.01329077,  0.33684243,  0.68697562,  1.03710882,  1.38724202,
         1.73737522]),
 <a list of 10 Patch objects>)
../../../_images/contents_notebooks_pandas_Standardize_other_26_1.png

累積構成比のための処理

In [98]:

columns = list("def")
normalized_df = df[columns].div(df[columns].sum())
print(normalized_df.sum())
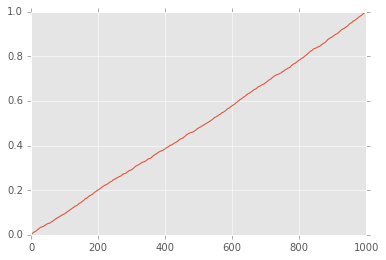
normalized_df["f"].cumsum().plot()


d    1
e    1
f    1
dtype: float64

Out[98]:

<matplotlib.axes._subplots.AxesSubplot at 0x11e117240>
../../../_images/contents_notebooks_pandas_Standardize_other_28_2.png

分布

http://docs.scipy.org/doc/numpy/reference/routines.random.html#distributions

name arguments
beta (a, b[, size])
binomial (n, p[, size])
chisquare (df[, size])
dirichlet (alpha[, size])
exponential ([scale, size])
f (dfnum, dfden[, size])
gamma (shape[, scale, size])
geometric (p[, size])
gumbel ([loc, scale, size])
hypergeometric (ngood, nbad, nsample[, size])
laplace ([loc, scale, size])
logistic ([loc, scale, size])
lognormal ([mean, sigma, size])
logseries (p[, size])
multinomial (n, pvals[, size])
multivariate_normal (mean, cov[, size])
negative_binomial (n, p[, size])
noncentral_chisquare (df, nonc[, size])
noncentral_f (dfnum, dfden, nonc[, size])
normal ([loc, scale, size])
pareto (a[, size])
poisson ([lam, size])
power (a[, size])
rayleigh ([scale, size])
standard_cauchy ([size])
standard_exponential ([size])
standard_gamma (shape[, size])
standard_normal ([size])
standard_t (df[, size])
triangular (left, mode, right[, size])
uniform ([low, high, size])
vonmises (mu, kappa[, size])
wald (mean, scale[, size])
weibull (a[, size])
zipf (a[, size])

formula式

  • Rのあれ
  • patsyというpydata提供のモジュール
  • statsmodelsにformulaあったなぁと調べたら、これだった
In [152]:

import patsy
patsy.dmatrices("c ~ .", df, return_type="dataframe")


  File "<unknown>", line 1
    .
    ^
SyntaxError: invalid syntax


In [116]:

y, X = patsy.dmatrices("c ~ a + b + d + e + f", df, return_type="dataframe")
X.head()

Out[116]:
Intercept b[T.b] b[T.c] b[T.d] b[T.e] b[T.f] b[T.g] b[T.h] b[T.i] b[T.j] ... b[T.t] b[T.u] b[T.v] b[T.w] b[T.x] b[T.y] a d e f
0 1 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 1 0.548814 -0.101697 53
1 1 1 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 2 0.715189 0.019279 76
2 1 0 1 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 3 0.602763 1.849591 54
3 1 0 0 1 0 0 0 0 0 0 ... 0 0 0 0 0 0 4 0.544883 -0.214167 94
4 1 0 0 0 1 0 0 0 0 0 ... 0 0 0 0 0 0 5 0.423655 -0.499017 68

5 rows × 29 columns

In [143]:

np.random.randint(0, 1+1, 50)

Out[143]:

array([0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1,
       1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0,
       1, 1, 1, 1])

In [156]:

df_ex = pd.DataFrame(
    {
        "a": np.random.randint(0, 3+1, 50),
        "b": range(50),
        "c": list("abcde") * 10,
        "d": [False, True] * 25,
        "y": np.random.randint(0, 1+1, 50)
    }
)
df_ex.describe()

Out[156]:
a b d y
count 50.000000 50.00000 50 50.000000
mean 1.460000 24.50000 0.5 0.520000
std 1.128662 14.57738 0.505076 0.504672
min 0.000000 0.00000 False 0.000000
25% 0.000000 12.25000 0 0.000000
50% 2.000000 24.50000 0.5 1.000000
75% 2.000000 36.75000 1 1.000000
max 3.000000 49.00000 True 1.000000 
In [157]:

outcome, predictors = patsy.dmatrices("y ~ C(a) + b + c + d",  df_ex, return_type="dataframe")
pd.concat([predictors, outcome], axis=1).head()


Out[157]:
Intercept C(a)[T.1] C(a)[T.2] C(a)[T.3] c[T.b] c[T.c] c[T.d] c[T.e] d[T.True] b y
0 1 0 0 0 0 0 0 0 0 0 1
1 1 1 0 0 1 0 0 0 1 1 0
2 1 0 1 0 0 1 0 0 0 2 1
3 1 0 1 0 0 0 1 0 1 3 1
4 1 1 0 0 0 0 0 1 0 4 0 
In [142]:

X.describe()

Out[142]:
Intercept C(a)[T.1] C(a)[T.2] C(a)[T.3] c[T.b] c[T.c] c[T.d] c[T.e] b
count 50 50.000000 50.000000 50.000000 50.000000 50.000000 50.000000 50.000000 50.00000
mean 1 0.220000 0.200000 0.320000 0.200000 0.200000 0.200000 0.200000 24.50000
std 0 0.418452 0.404061 0.471212 0.404061 0.404061 0.404061 0.404061 14.57738
min 1 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.00000
25% 1 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 12.25000
50% 1 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 24.50000
75% 1 0.000000 0.000000 1.000000 0.000000 0.000000 0.000000 0.000000 36.75000
max 1 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000 49.00000 
In [158]:

y, X = patsy.dmatrices("c ~ a + C(b) + d + e + f", df, return_type="dataframe")
X.head()

Out[158]:
Intercept C(b)[T.b] C(b)[T.c] C(b)[T.d] C(b)[T.e] C(b)[T.f] C(b)[T.g] C(b)[T.h] C(b)[T.i] C(b)[T.j] ... C(b)[T.t] C(b)[T.u] C(b)[T.v] C(b)[T.w] C(b)[T.x] C(b)[T.y] a d e f
0 1 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 1 0.548814 -0.101697 53
1 1 1 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 2 0.715189 0.019279 76
2 1 0 1 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 3 0.602763 1.849591 54
3 1 0 0 1 0 0 0 0 0 0 ... 0 0 0 0 0 0 4 0.544883 -0.214167 94
4 1 0 0 0 1 0 0 0 0 0 ... 0 0 0 0 0 0 5 0.423655 -0.499017 68

5 rows × 29 columns

In [159]:

y.head()

Out[159]:
c[1] c[2] c[3] c[4]
0 1 0 0 0
1 0 1 0 0
2 0 0 1 0
3 0 0 0 1
4 1 0 0 0 
In [160]:

np.ravel(y), len(np.ravel(y))

Out[160]:

(array([ 1.,  0.,  0., ...,  0.,  0.,  1.]), 4000)