corr_ratio_fvalue

In [1]:

%matplotlib inline
import numpy as np
import pandas as pd
import scipy.stats
import matplotlib.pyplot as plt
import seaborn as sns

In [2]:

# マンガでわかる統計学: p121-126
observed = pd.DataFrame({
    "1_t": [23, 26, 27, 28, np.nan, np.nan],
    "2_sha": [25, 26, 29, 32, 33, np.nan],
    "3_ba": [15, 16, 18, 22, 26, 29]
})
observed

Out[2]:
1_t 2_sha 3_ba
0 23.0 25.0 15
1 26.0 26.0 16
2 27.0 29.0 18
3 28.0 32.0 22
4 NaN 33.0 26
5 NaN NaN 29 
In [3]:

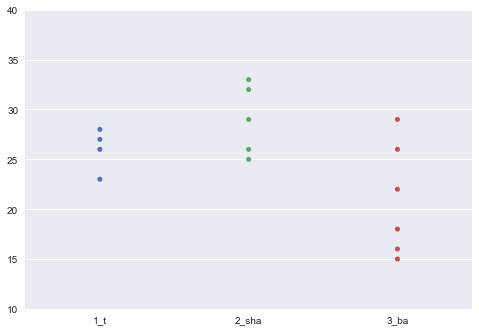
sns.swarmplot(data=observed)
plt.ylim(10, 40)

Out[3]:

(10, 40)
../../../../_images/contents_notebooks_scipy_stats_corr_ratio_fvalue_3_1.png 
In [4]:

def corr_ratio(observed):
    # 級内変動
    ssw = ((observed - observed.mean()) ** 2).sum().sum()

    # 級間変動
    ssb = (observed.count() * ((observed.mean() - np.nanmean(observed)) ** 2)).sum()

    # sst
    sst = ((observed - np.nanmean(observed)) ** 2).sum().sum()

    # 相関比
    ratio = ssb / (ssb + ssw)

    # F
    dfn = observed.shape[1] - 1
    dfd = (observed.count() - 1).sum()
    f = (ssb / dfn) / (ssw / dfd)

    # p
    p = scipy.stats.f.sf(f, dfn, dfd)

    return (ssw, ssb, ratio, sst, f, p)


In [5]:

corr_ratio(observed)

Out[5]:

(224.0,
 180.0,
 0.44554455445544555,
 404.0,
 4.821428571428571,
 0.029053597747097693)

In [6]:

scipy.stats.f_oneway(observed["1_t"].dropna(),
                             observed["2_sha"].dropna(),
                             observed["3_ba"].dropna())

Out[6]:

F_onewayResult(statistic=4.8214285714285712, pvalue=0.029053597747097693)

In [7]:

# https://en.wikipedia.org/wiki/Correlation_ratio
df_math_scores = pd.DataFrame({
    "Algebra": [45, 70, 29, 15, 21, np.nan],
    "Geometry": [40, 20, 30, 42, np.nan, np.nan],
    "Statistics": [65, 95, 80, 70, 85, 73]
})
\[\eta ^{2}={\frac {6780}{9640}}=0.7033\ldots\]
In [8]:

corr_ratio(df_math_scores)

Out[8]:

(2860.0,
 6780.0,
 0.7033195020746889,
 9640.0,
 14.223776223776223,
 0.000681920890799404)

In [9]:

sum(corr_ratio(df_math_scores)[:2])

Out[9]:

9640.0

In [ ]: