numpy¶
In [1]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
In [2]:
np.random.seed(0)
x = np.arange(-5, 5, 0.1)
y = np.arange(-5, 5, 0.1)
xx, yy = np.meshgrid(x, y)#, sparse=True)
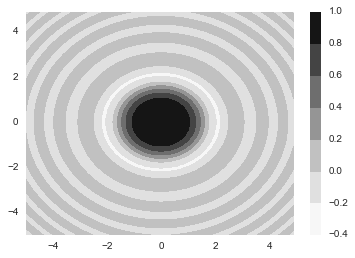
z = np.sin(xx**2 + yy**2) / (xx**2 + yy**2)
h = plt.contourf(x,y,z)
plt.colorbar(h)
Out[2]:
<matplotlib.colorbar.Colorbar at 0x11993edd8>
In [3]:
xx_df = pd.DataFrame(xx)
yy_df = pd.DataFrame(yy)
xx_df_drop_duplicated = xx_df.drop_duplicates()
print(len(xx_df), len(yy_df))
print((xx_df_drop_duplicated == yy_df.T.drop_duplicates()).T.drop_duplicates())
xx_df_drop_duplicated
100 100
0
0 True
Out[3]:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -5.0 | -4.9 | -4.8 | -4.7 | -4.6 | -4.5 | -4.4 | -4.3 | -4.2 | -4.1 | ... | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 |
1 rows × 100 columns
In [4]:
xx_sp, yy_sp = np.meshgrid(x, y, sparse=True)
pd.DataFrame(xx_sp == yy_sp.T).sum(axis=1), pd.DataFrame(xx_sp == x).sum(axis=1)
Out[4]:
(0 100
dtype: int64, 0 100
dtype: int64)
In [5]:
x, y = np.meshgrid([1,2,3,4], [5,6,7])
x_sp, y_sp = np.meshgrid([1,2,3,4], [5,6,7], sparse=True)
pd.concat(
[pd.DataFrame(x), pd.DataFrame(y), pd.DataFrame(x + y)], axis=1)
x, y, z = np.meshgrid([1,2,3,4], [5,6,7], [8, 9])
x_sp, y_sp, z_sp = np.meshgrid([1,2,3,4], [5,6,7], [8,9], sparse=True)
pd.concat(
[pd.Panel(x), pd.Panel(y), pd.Panel(z), pd.Panel(x + y + z)], axis=1)
Out[5]:
<class 'pandas.core.panel.Panel'>
Dimensions: 3 (items) x 16 (major_axis) x 2 (minor_axis)
Items axis: 0 to 2
Major_axis axis: 0 to 3
Minor_axis axis: 0 to 1
In [6]:
[(v) for l, v in pd.Panel(y).iteritems()]
Out[6]:
[ 0 1
0 5 5
1 5 5
2 5 5
3 5 5, 0 1
0 6 6
1 6 6
2 6 6
3 6 6, 0 1
0 7 7
1 7 7
2 7 7
3 7 7]
In [7]:
pd.concat(
[pd.DataFrame(x_sp), pd.DataFrame(y_sp.T), pd.DataFrame(x_sp + y_sp)])
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-7-155b265fd782> in <module>()
1 pd.concat(
----> 2 [pd.DataFrame(x_sp), pd.DataFrame(y_sp.T), pd.DataFrame(x_sp + y_sp)])
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/pandas/core/frame.py in __init__(self, data, index, columns, dtype, copy)
252 else:
253 mgr = self._init_ndarray(data, index, columns, dtype=dtype,
--> 254 copy=copy)
255 elif isinstance(data, (list, types.GeneratorType)):
256 if isinstance(data, types.GeneratorType):
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/pandas/core/frame.py in _init_ndarray(self, values, index, columns, dtype, copy)
409 # by definition an array here
410 # the dtypes will be coerced to a single dtype
--> 411 values = _prep_ndarray(values, copy=copy)
412
413 if dtype is not None:
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/pandas/core/frame.py in _prep_ndarray(values, copy)
5332 values = values.reshape((values.shape[0], 1))
5333 elif values.ndim != 2:
-> 5334 raise ValueError('Must pass 2-d input')
5335
5336 return values
ValueError: Must pass 2-d input
In [17]:
x_sp
Out[17]:
array([[[1],
[2],
[3],
[4]]])
In [18]:
y_sp.T
Out[18]:
array([[[5, 6, 7]]])
In [19]:
x_sp + y_sp
Out[19]:
array([[[ 6],
[ 7],
[ 8],
[ 9]],
[[ 7],
[ 8],
[ 9],
[10]],
[[ 8],
[ 9],
[10],
[11]]])
In [15]:
[pd.DataFrame(x_sp), pd.DataFrame(y_sp.T), pd.DataFrame(x_sp + y_sp)]
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-15-c073deaeb308> in <module>()
----> 1 [pd.DataFrame(x_sp), pd.DataFrame(y_sp.T), pd.DataFrame(x_sp + y_sp)]
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/pandas/core/frame.py in __init__(self, data, index, columns, dtype, copy)
252 else:
253 mgr = self._init_ndarray(data, index, columns, dtype=dtype,
--> 254 copy=copy)
255 elif isinstance(data, (list, types.GeneratorType)):
256 if isinstance(data, types.GeneratorType):
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/pandas/core/frame.py in _init_ndarray(self, values, index, columns, dtype, copy)
409 # by definition an array here
410 # the dtypes will be coerced to a single dtype
--> 411 values = _prep_ndarray(values, copy=copy)
412
413 if dtype is not None:
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/pandas/core/frame.py in _prep_ndarray(values, copy)
5332 values = values.reshape((values.shape[0], 1))
5333 elif values.ndim != 2:
-> 5334 raise ValueError('Must pass 2-d input')
5335
5336 return values
ValueError: Must pass 2-d input
In [20]:
contourf = plt.contourf(x, y, x + y)
plt.colorbar(contourf)
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-20-16b509980145> in <module>()
----> 1 contourf = plt.contourf(x, y, x + y)
2 plt.colorbar(contourf)
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/matplotlib/pyplot.py in contourf(*args, **kwargs)
2781 ax.hold(hold)
2782 try:
-> 2783 ret = ax.contourf(*args, **kwargs)
2784 finally:
2785 ax.hold(washold)
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/matplotlib/__init__.py in inner(ax, *args, **kwargs)
1810 warnings.warn(msg % (label_namer, func.__name__),
1811 RuntimeWarning, stacklevel=2)
-> 1812 return func(ax, *args, **kwargs)
1813 pre_doc = inner.__doc__
1814 if pre_doc is None:
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/matplotlib/axes/_axes.py in contourf(self, *args, **kwargs)
5650 self.cla()
5651 kwargs['filled'] = True
-> 5652 return mcontour.QuadContourSet(self, *args, **kwargs)
5653 contourf.__doc__ = mcontour.QuadContourSet.contour_doc
5654
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/matplotlib/contour.py in __init__(self, ax, *args, **kwargs)
1422 are described in QuadContourSet.contour_doc.
1423 """
-> 1424 ContourSet.__init__(self, ax, *args, **kwargs)
1425
1426 def _process_args(self, *args, **kwargs):
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/matplotlib/contour.py in __init__(self, ax, *args, **kwargs)
861 self._transform = kwargs.get('transform', None)
862
--> 863 self._process_args(*args, **kwargs)
864 self._process_levels()
865
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/matplotlib/contour.py in _process_args(self, *args, **kwargs)
1443 self._corner_mask = mpl.rcParams['contour.corner_mask']
1444
-> 1445 x, y, z = self._contour_args(args, kwargs)
1446
1447 _mask = ma.getmask(z)
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/matplotlib/contour.py in _contour_args(self, args, kwargs)
1526 args = args[1:]
1527 elif Nargs <= 4:
-> 1528 x, y, z = self._check_xyz(args[:3], kwargs)
1529 args = args[3:]
1530 else:
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/matplotlib/contour.py in _check_xyz(self, args, kwargs)
1560
1561 if z.ndim != 2:
-> 1562 raise TypeError("Input z must be a 2D array.")
1563 else:
1564 Ny, Nx = z.shape
TypeError: Input z must be a 2D array.
In [21]:
ary = np.array([1,2,3,4,5,6,7,8]).reshape(2,2,2).T
ary
Out[21]:
array([[[1, 5],
[3, 7]],
[[2, 6],
[4, 8]]])
In [22]:
ary.ravel()
Out[22]:
array([1, 5, 3, 7, 2, 6, 4, 8])
In [23]:
# http://docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.c_.html
# http://docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.r_.html
# http://docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.concatenate.html
#
ar1 = np.array(range(6)).reshape(2, 3)
ar2 = np.array(range(1, 7)).reshape(2, 3)
c_ = np.c_[ar1, ar2]
r_ = np.r_[ar1, ar2]
concat_r = np.concatenate([ar1, ar2])
concat_c = np.concatenate([ar1, ar2], axis=1)
pd.DataFrame(c_)
Out[23]:
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 1 | 2 | 3 |
| 1 | 3 | 4 | 5 | 4 | 5 | 6 |
In [24]:
pd.DataFrame(r_)
Out[24]:
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 0 | 1 | 2 |
| 1 | 3 | 4 | 5 |
| 2 | 1 | 2 | 3 |
| 3 | 4 | 5 | 6 |
In [25]:
(pd.DataFrame(r_) == pd.DataFrame(concat_r)).all().sum()
Out[25]:
3
In [26]:
(pd.DataFrame(c_) == pd.DataFrame(concat_c)).all().sum()
Out[26]:
6
In [9]:
Function Description
diag 対角要素を抜き出す
dot 内積
trace 対角要素の和
det 行列式
eig 固有値と固有ベクトルへ分解
inv 転置
pinv ムーア-ペンローズの擬似逆行列
qr QR分解
svd SVD分解
solve Aが正方行列のときAx=bのxを求める
stsq 最小二乗解を計算
File "<ipython-input-9-01ed6ad0e591>", line 1
Function Description
^
SyntaxError: invalid syntax
In [87]:
a
Out[87]:
array([[1, 1],
[2, 4]])
In [86]:
np.diag(a)
Out[86]:
array([1, 4])
In [91]:
a.diagonal()
Out[91]:
array([1, 4])
In [89]:
np.dot(a, a)
Out[89]:
array([[ 3, 5],
[10, 18]])
In [90]:
a.dot(a)
Out[90]:
array([[ 3, 5],
[10, 18]])
In [92]:
a @ a
Out[92]:
array([[ 3, 5],
[10, 18]])
In [88]:
np.trace(a)
Out[88]:
5
In [93]:
a.trace()
Out[93]:
5
In [96]:
np.linalg.det(a)
Out[96]:
2.0
In [97]:
np.linalg.eig(a)
Out[97]:
(array([ 0.43844719, 4.56155281]), array([[-0.87192821, -0.27032301],
[ 0.48963374, -0.96276969]]))
In [100]:
np.linalg.inv(a)
Out[100]:
array([[ 2. , -0.5],
[-1. , 0.5]])
In [106]:
np.linalg.pinv(a)
Out[106]:
array([[ 2. , -0.5],
[-1. , 0.5]])
In [107]:
np.linalg.qr(a)
Out[107]:
(array([[-0.4472136 , -0.89442719],
[-0.89442719, 0.4472136 ]]), array([[-2.23606798, -4.02492236],
[ 0. , 0.89442719]]))
In [109]:
np.linalg.svd(a)
Out[109]:
(array([[-0.28978415, -0.95709203],
[-0.95709203, 0.28978415]]),
array([ 4.6708301 , 0.42818941]),
array([[-0.47185793, -0.8816746 ],
[-0.8816746 , 0.47185793]]))
In [108]:
np.linalg.solve(a, a)
Out[108]:
array([[ 1., 0.],
[-0., 1.]])
In [112]:
np.linalg.lstsq(a, a)
Out[112]:
(array([[ 1.00000000e+00, 3.31004554e-16],
[ 2.75837128e-16, 1.00000000e+00]]),
array([], dtype=float64),
2,
array([ 4.6708301 , 0.42818941]))
In [98]:
np.invert(a)
Out[98]:
array([[-2, -2],
[-3, -5]])
In [ ]:
"""
x + y = 3
2x + 4y = 10
([[1, 1], ([[x], ([[3],
* =
[2, 4]]) [y]]) [10]])
"""
In [35]:
np.arange(4).reshape(2, 2)
Out[35]:
array([[0, 1],
[2, 3]])
In [40]:
a = np.array([[1, 1], [2, 4]])
b = np.array([[3], [10]])
print(a, "\n"*2, b)
[[1 1]
[2 4]]
[[ 3]
[10]]
In [53]:
type(a)
?np.ndarray
In [42]:
np.linalg.solve(a, b)
Out[42]:
array([[ 1.],
[ 2.]])
In [45]:
np.linalg.inv(a).dot(b)
Out[45]:
array([[ 1.],
[ 2.]])
In [49]:
# http://docs.scipy.org/doc/numpy/reference/generated/numpy.multiply.html
np.multiply(np.linalg.inv(a), b)
Out[49]:
array([[ 6. , -1.5],
[-10. , 5. ]])
In [46]:
np.linalg.inv(a) @ b
Out[46]:
array([[ 1.],
[ 2.]])
In [47]:
np.matrix(np.linalg.inv(a)) * b
Out[47]:
matrix([[ 1.],
[ 2.]])
In [54]:
a * b
Out[54]:
array([[ 3, 3],
[20, 40]])
In [55]:
a.dot(b)
Out[55]:
array([[13],
[46]])
In [58]:
b.dot(b.T)
Out[58]:
array([[ 9, 30],
[ 30, 100]])
In [59]:
b.T.dot(b)
Out[59]:
array([[109]])
In [65]:
np.inner(b, b)
Out[65]:
array([[ 9, 30],
[ 30, 100]])
In [66]:
np.inner(b.T, b.T)
Out[66]:
array([[109]])
In [62]:
outer_ab = np.outer(a, b)
outer_ba = np.outer(b, a)
outer_ab == outer_ba.T
Out[62]:
array([[ True, True],
[ True, True],
[ True, True],
[ True, True]], dtype=bool)
In [63]:
outer_ab
Out[63]:
array([[ 3, 10],
[ 3, 10],
[ 6, 20],
[12, 40]])
In [67]:
np.dot(a.T, b)
Out[67]:
array([[23],
[43]])
In [71]:
# ?np.outer
np.outer(np.array(['a', 'b', 'c'], dtype=object), [1, 2, 3])
Out[71]:
array([['a', 'aa', 'aaa'],
['b', 'bb', 'bbb'],
['c', 'cc', 'ccc']], dtype=object)
In [72]:
np.outer(np.array([1,2,3]), [1, 2, 3])
Out[72]:
array([[1, 2, 3],
[2, 4, 6],
[3, 6, 9]])
In [81]:
np.array([1,2,3]).reshape(3, 1)
Out[81]:
array([[1],
[2],
[3]])
In [84]:
np.array([1,2,3]).reshape(3, 1).dot(np.array([1,2,3]).reshape(1, 3))
Out[84]:
array([[1, 2, 3],
[2, 4, 6],
[3, 6, 9]])
In [27]:
sns.plt.plot([0,1], [0,1]); sns.plt.title('tofu - 豆腐')
Out[27]:
<matplotlib.text.Text at 0x11a4d1080>
In [28]:
sns.set(font='IPAexGothic')
sns.plt.plot([0,1], [0,1]); sns.plt.title('tofu - 豆腐')
Out[28]:
<matplotlib.text.Text at 0x11a530f28>
In [ ]:
In [29]:
import matplotlib.font_manager as fm
import pandas as pd
# フォントの一覧
fonts = fm.findSystemFonts()
fonts
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/matplotlib/font_manager.py:273: UserWarning: Matplotlib is building the font cache using fc-list. This may take a moment.
warnings.warn('Matplotlib is building the font cache using fc-list. This may take a moment.')
Out[29]:
['/Library/Fonts/Microsoft/Candara Italic.ttf',
'/Library/Fonts/Farisi.ttf',
'/Library/Fonts/Microsoft/MS Mincho.ttf',
'/Library/Fonts/PCmyoungjo.ttf',
'/System/Library/Fonts/Apple Braille Outline 8 Dot.ttf',
'/Users/knt/Library/Fonts/Ricty-Bold.ttf',
'/System/Library/Fonts/SFNSText-Bold.otf',
'/Library/Fonts/Kokonor.ttf',
'/Library/Fonts/Microsoft/Tw Cen MT Bold.ttf',
'/System/Library/Fonts/SFNSDisplay-Light.otf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMBatnanBold.otf',
'/Library/Fonts/Tahoma Bold.ttf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMMardinBold.otf',
'/System/Library/Fonts/SFNSDisplay-Medium.otf',
'/Library/Fonts/Silom.ttf',
'/Library/Fonts/Microsoft/MS Reference Sans Serif.ttf',
'/Library/Fonts/AppleMyungjo.ttf',
'/Library/Fonts/Chalkduster.ttf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMAntioch.otf',
'/Library/Fonts/Microsoft/Verdana Italic.ttf',
'/Library/Fonts/Microsoft/Meiryo Bold.ttf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMMalankara.otf',
'/Library/Fonts/Microsoft/Gulim.ttf',
'/Library/Fonts/Mishafi.ttf',
'/Library/Fonts/STIXIntDReg.otf',
'/Library/Fonts/Microsoft/Bookshelf Symbol 7.ttf',
'/Library/Fonts/Courier New Bold.ttf',
'/usr/local/share/fonts/migu-1m-bold.ttf',
'/Library/Fonts/Microsoft/Verdana Bold Italic.ttf',
'/Library/Fonts/STIXIntUpDBol.otf',
'/Library/Fonts/Microsoft/taile.ttf',
'/Library/Fonts/Khmer Sangam MN.ttf',
'/Library/Fonts/Microsoft/Perpetua Italic.ttf',
'/Library/Fonts/Microsoft/Corbel Bold Italic.ttf',
'/System/Library/Fonts/SFNSText-BoldG1.otf',
'/Library/Fonts/Microsoft/Candara.ttf',
'/Library/Fonts/STIXIntDBol.otf',
'/usr/local/share/fonts/Ricty-Bold.ttf',
'/Library/Fonts/InaiMathi.ttf',
'/Library/Fonts/Microsoft/Batang.ttf',
'/Library/Fonts/STIXIntSmReg.otf',
'/Library/Fonts/Brush Script.ttf',
'/System/Library/Fonts/SFNSText-BoldItalicG3.otf',
'/System/Library/Fonts/SFNSText-RegularItalicG1.otf',
'/Library/Fonts/Bodoni 72 Smallcaps Book.ttf',
'/Library/Fonts/Microsoft/Perpetua Bold.ttf',
'/Library/Fonts/Microsoft/Calibri Bold Italic.ttf',
'/usr/X11/lib/X11/fonts/TTF/luximr.ttf',
'/Library/Fonts/Microsoft/MS Reference Specialty.ttf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMJerusalemBold.otf',
'/System/Library/Fonts/SFNSText-BoldItalicG1.otf',
'/Library/Fonts/Microsoft/Candara Bold Italic.ttf',
'/Library/Fonts/STIXIntUpSmBol.otf',
'/Library/Fonts/Arial Narrow Italic.ttf',
'/Library/Fonts/Microsoft/Meiryo.ttf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMMardin.otf',
'/System/Library/Fonts/Apple Braille Outline 6 Dot.ttf',
'/System/Library/Fonts/Symbol.ttf',
'/Library/Fonts/Microsoft/Gill Sans MT Bold.ttf',
'/Library/Fonts/Trebuchet MS Italic.ttf',
'/usr/X11/lib/X11/fonts/TTF/VeraSeBd.ttf',
'/Library/Fonts/Arial Black.ttf',
'/System/Library/Fonts/SFNSText-BoldItalic.otf',
'/Library/Fonts/Microsoft/Consolas Italic.ttf',
'/Library/Fonts/Bradley Hand Bold.ttf',
'/Library/Fonts/Microsoft/Arial Bold Italic.ttf',
'/Library/Fonts/DIN Alternate Bold.ttf',
'/System/Library/Fonts/SFNSText-Medium.otf',
'/Library/Fonts/Microsoft/Candara Bold.ttf',
'/Library/Fonts/Arial Unicode.ttf',
'/Library/Fonts/Georgia Bold Italic.ttf',
'/Library/Fonts/STIXNonUni.otf',
'/Library/Fonts/STIXNonUniBol.otf',
'/Library/Fonts/Microsoft/Cambria Bold Italic.ttf',
'/Library/Fonts/STIXIntUpReg.otf',
'/Users/knt/Library/Fonts/Ricty-Regular.ttf',
'/Library/Fonts/Microsoft/Palatino Linotype Italic.ttf',
'/Library/Fonts/Mishafi Gold.ttf',
'/Library/Fonts/Yu Gothic Medium.otf',
'/Library/Fonts/Verdana Bold Italic.ttf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMQenNeshrin.otf',
'/Library/Fonts/Times New Roman Bold.ttf',
'/Library/Fonts/Microsoft/Franklin Gothic Book Italic.ttf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMJerusalem.otf',
'/Library/Fonts/Microsoft/MS PGothic.ttf',
'/Library/Fonts/Microsoft/Calibri.ttf',
'/Library/Fonts/Arial Rounded Bold.ttf',
'/Library/Fonts/Microsoft/Franklin Gothic Medium Italic.ttf',
'/Library/Fonts/儷宋 Pro.ttf',
'/Library/Fonts/儷黑 Pro.ttf',
'/usr/X11/lib/X11/fonts/TTF/GohaTibebZemen.ttf',
'/Library/Fonts/Andale Mono.ttf',
'/Library/Fonts/Impact.ttf',
'/usr/local/share/fonts/Inconsolata.otf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMCtesiphon.otf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMEdessa.otf',
'/Library/Fonts/Microsoft/SimSun.ttf',
'/Library/Fonts/Microsoft/Times New Roman Bold.ttf',
'/Library/Fonts/Times New Roman Italic.ttf',
'/Library/Fonts/Ayuthaya.ttf',
'/usr/X11/lib/X11/fonts/TTF/VeraMoIt.ttf',
'/usr/X11/lib/X11/fonts/TTF/luximri.ttf',
'/Library/Fonts/Microsoft/Gabriola.ttf',
'/Library/Fonts/Microsoft/msyi.ttf',
'/Library/Fonts/华文细黑.ttf',
'/usr/local/share/fonts/RictyDiscord-Bold.ttf',
'/Library/Fonts/STIXSizOneSymBol.otf',
'/System/Library/Fonts/Apple Braille Pinpoint 8 Dot.ttf',
'/Library/Fonts/Trebuchet MS.ttf',
'/Library/Fonts/Microsoft/Consolas Bold.ttf',
'/Library/Fonts/STIXIntUpDReg.otf',
'/Library/Fonts/DIN Condensed Bold.ttf',
'/Library/Fonts/Microsoft/Tw Cen MT Italic.ttf',
'/usr/X11/lib/X11/fonts/TTF/luxirri.ttf',
'/Library/Fonts/WeibeiSC-Bold.otf',
'/Library/Fonts/PlantagenetCherokee.ttf',
'/Library/Fonts/Arial.ttf',
'/System/Library/Fonts/SFNSText-SemiboldItalic.otf',
'/Library/Fonts/STIXGeneralBolIta.otf',
'/System/Library/Fonts/SFNSText-RegularItalic.otf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMAdiabene.otf',
'/Library/Fonts/Microsoft/HGRSMP.TTF',
'/Library/Fonts/Sathu.ttf',
'/Library/Fonts/Microsoft/Tw Cen MT Bold Italic.ttf',
'/System/Library/Fonts/SFNSDisplay-Semibold.otf',
'/Library/Fonts/Microsoft/Arial Bold.ttf',
'/Library/Fonts/Microsoft/Times New Roman.ttf',
'/System/Library/Fonts/SFNSDisplay-Heavy.otf',
'/System/Library/Fonts/SFNSText-MediumItalic.otf',
'/Library/Fonts/AppleGothic.ttf',
'/Library/Fonts/Microsoft/Wingdings 3.ttf',
'/System/Library/Fonts/SFNSDisplay-Black.otf',
'/Library/Fonts/Microsoft/SimSun-ExtB.ttf',
'/Library/Fonts/Apple Chancery.ttf',
'/Library/Fonts/STIXSizThreeSymBol.otf',
'/Library/Fonts/Gurmukhi.ttf',
'/usr/X11/lib/X11/fonts/TTF/luxisri.ttf',
'/Library/Fonts/YuppySC-Regular.otf',
'/Library/Fonts/Osaka.ttf',
'/Library/Fonts/Microsoft/Arial.ttf',
'/usr/X11/lib/X11/fonts/TTF/VeraSe.ttf',
'/Library/Fonts/Microsoft/Constantia.ttf',
'/usr/X11/lib/X11/fonts/TTF/VeraIt.ttf',
'/Library/Fonts/Microsoft/Verdana.ttf',
'/Library/Fonts/Microsoft/Brush Script.ttf',
'/Library/Fonts/Microsoft/Calibri Bold.ttf',
'/System/Library/Fonts/SFNSText-HeavyItalic.otf',
'/Library/Fonts/Arial Narrow.ttf',
'/Library/Fonts/Verdana.ttf',
'/Library/Fonts/STIXGeneralBol.otf',
'/Library/Fonts/Georgia.ttf',
'/Library/Fonts/Microsoft/Cambria Italic.ttf',
'/Library/Fonts/SignPainter.otf',
'/Library/Fonts/Times New Roman Bold Italic.ttf',
'/Library/Fonts/Microsoft/Constantia Italic.ttf',
'/Library/Fonts/Georgia Italic.ttf',
'/usr/X11/lib/X11/fonts/TTF/luximbi.ttf',
'/System/Library/Fonts/SFNSText-BoldItalicG2.otf',
'/usr/X11/lib/X11/fonts/TTF/luxirbi.ttf',
'/Library/Fonts/Hoefler Text Ornaments.ttf',
'/Library/Fonts/Microsoft/MS Gothic.ttf',
'/Library/Fonts/Microsoft/Verdana Bold.ttf',
'/Library/Fonts/Microsoft/SimHei.ttf',
'/Library/Fonts/STIXSizFiveSymReg.otf',
'/Library/Fonts/Microsoft/mingliu_hkscs.ttf',
'/usr/X11/lib/X11/fonts/TTF/luxisb.ttf',
'/Library/Fonts/Microsoft/himalaya.ttf',
'/System/Library/Fonts/Apple Braille.ttf',
'/usr/X11/lib/X11/fonts/TTF/VeraMoBd.ttf',
'/Library/Fonts/Microsoft/MingLiU-ExtB.ttf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMUrhoy.otf',
'/Library/Fonts/Skia.ttf',
'/Library/Fonts/Wingdings 3.ttf',
'/Library/Fonts/STIXSizFourSymReg.otf',
'/usr/X11/lib/X11/fonts/OTF/GohaTibebZemen.otf',
'/Library/Fonts/Microsoft/Lucida Sans Unicode.ttf',
'/System/Library/Fonts/SFNSText-Light.otf',
'/Library/Fonts/Krungthep.ttf',
'/Library/Fonts/Trattatello.ttf',
'/Library/Fonts/Microsoft/Corbel.ttf',
'/System/Library/Fonts/SFNSText-Regular.otf',
'/Library/Fonts/Microsoft Sans Serif.ttf',
'/Library/Fonts/Arial Bold.ttf',
'/Library/Fonts/Microsoft/Franklin Gothic Medium.ttf',
'/usr/X11/lib/X11/fonts/TTF/luxirr.ttf',
'/Library/Fonts/Microsoft/Cambria.ttf',
'/Library/Fonts/Webdings.ttf',
'/Library/Fonts/NISC18030.ttf',
'/System/Library/Fonts/Apple Braille Pinpoint 6 Dot.ttf',
'/Library/Fonts/STIXVar.otf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMTalada.otf',
'/Library/Fonts/Microsoft/Palatino Linotype.ttf',
'/Library/Fonts/Courier New.ttf',
'/Library/Fonts/STIXSizOneSymReg.otf',
'/Library/Fonts/WawaTC-Regular.otf',
'/Library/Fonts/Gungseouche.ttf',
'/System/Library/Fonts/SFNSText-Heavy.otf',
'/usr/local/share/fonts/Ricty-Regular.ttf',
'/Library/Fonts/Comic Sans MS.ttf',
'/Library/Fonts/Yu Gothic Bold.otf',
'/Library/Fonts/Verdana Italic.ttf',
'/Library/Fonts/Tahoma.ttf',
'/Library/Fonts/Arial Narrow Bold.ttf',
'/System/Library/Fonts/SFNSText-BoldG2.otf',
'/Library/Fonts/Bodoni Ornaments.ttf',
'/Library/Fonts/Microsoft/MS PMincho.ttf',
'/Library/Fonts/STIXGeneral.otf',
'/System/Library/Fonts/SFNSDisplay-Regular.otf',
'/Library/Fonts/Microsoft/Times New Roman Bold Italic.ttf',
'/System/Library/Fonts/SFNSText-RegularG3.otf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMKharput.otf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMUrhoyBold.otf',
'/System/Library/Fonts/Keyboard.ttf',
'/Library/Fonts/Microsoft/Palatino Linotype Bold Italic.ttf',
'/Library/Fonts/Arial Italic.ttf',
'/Library/Fonts/Courier New Italic.ttf',
'/Library/Fonts/Times New Roman.ttf',
'/Library/Fonts/Wingdings.ttf',
'/usr/X11/lib/X11/fonts/TTF/Vera.ttf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMMidyat.otf',
'/Library/Fonts/Herculanum.ttf',
'/Library/Fonts/HeadlineA.ttf',
'/System/Library/Fonts/SFNSDisplay-Thin.otf',
'/usr/X11/lib/X11/fonts/TTF/luximb.ttf',
'/Library/Fonts/Microsoft/Gill Sans MT.ttf',
'/usr/X11/lib/X11/fonts/TTF/VeraMono.ttf',
'/Library/Fonts/STIXIntSmBol.otf',
'/System/Library/Fonts/SFNSText-RegularG2.otf',
'/Library/Fonts/Microsoft/Calibri Italic.ttf',
'/usr/local/share/fonts/RictyDiscord-Regular.ttf',
'/System/Library/Fonts/SFNSText-Semibold.otf',
'/Library/Fonts/Microsoft/Consolas.ttf',
'/usr/X11/lib/X11/fonts/TTF/luxirb.ttf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMJerusalemItalic.otf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMBatnan.otf',
'/Library/Fonts/Verdana Bold.ttf',
'/Library/Fonts/BigCaslon.ttf',
'/System/Library/Fonts/Apple Color Emoji.ttf',
'/Library/Fonts/Microsoft/Meiryo Bold Italic.ttf',
'/Library/Fonts/Microsoft/Corbel Bold.ttf',
'/Library/Fonts/Comic Sans MS Bold.ttf',
'/usr/local/share/fonts/migu-1m-regular.ttf',
'/Library/Fonts/STIXSizThreeSymReg.otf',
'/Library/Fonts/Microsoft/Gill Sans MT Bold Italic.ttf',
'/Library/Fonts/Microsoft/MingLiU.ttf',
'/System/Library/Fonts/SFNSDisplay-Ultralight.otf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMNisibinOutline.otf',
'/Library/Fonts/Microsoft/Perpetua.ttf',
'/Library/Fonts/Microsoft/Wingdings.ttf',
'/Library/Fonts/Microsoft/Consolas Bold Italic.ttf',
'/Library/Fonts/Georgia Bold.ttf',
'/Library/Fonts/STIXNonUniIta.otf',
'/Library/Fonts/Luminari.ttf',
'/Library/Fonts/Microsoft/monbaiti.ttf',
'/Library/Fonts/Microsoft/Gill Sans MT Italic.ttf',
'/Library/Fonts/Microsoft/PMingLiU.ttf',
'/Library/Fonts/Microsoft/Tw Cen MT.ttf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMTurAbdin.otf',
'/Users/knt/Library/Fonts/RictyDiscord-Bold.ttf',
'/Library/Fonts/Microsoft/Constantia Bold.ttf',
'/Library/Fonts/Microsoft/Meiryo Italic.ttf',
'/Library/Fonts/Microsoft/Palatino Linotype Bold.ttf',
'/Library/Fonts/Microsoft/Wingdings 2.ttf',
'/Library/Fonts/Microsoft/Cambria Bold.ttf',
'/Library/Fonts/Arial Bold Italic.ttf',
'/Library/Fonts/Microsoft/Times New Roman Italic.ttf',
'/Library/Fonts/华文仿宋.ttf',
'/Library/Fonts/Wingdings 2.ttf',
'/usr/X11/lib/X11/fonts/TTF/luxisbi.ttf',
'/Library/Fonts/Trebuchet MS Bold.ttf',
'/usr/X11/lib/X11/fonts/TTF/luxisr.ttf',
'/Library/Fonts/WawaSC-Regular.otf',
'/Library/Fonts/STIXGeneralItalic.otf',
'/Library/Fonts/STIXIntUpBol.otf',
'/Users/knt/Library/Fonts/RictyDiscord-Regular.ttf',
'/Library/Fonts/OsakaMono.ttf',
'/System/Library/Fonts/SFNSText-BoldG3.otf',
'/Library/Fonts/Diwan Thuluth.ttf',
'/usr/X11/lib/X11/fonts/TTF/VeraMoBI.ttf',
'/Library/Fonts/Lao Sangam MN.ttf',
'/Library/Fonts/Microsoft/Marlett.ttf',
'/Library/Fonts/Microsoft/Franklin Gothic Book.ttf',
'/Library/Fonts/Microsoft/Perpetua Bold Italic.ttf',
'/Library/Fonts/STIXNonUniBolIta.otf',
'/Library/Fonts/Zapfino.ttf',
'/Library/Fonts/Microsoft/Arial Italic.ttf',
'/Library/Fonts/Arial Narrow Bold Italic.ttf',
'/Library/Fonts/Pilgiche.ttf',
'/System/Library/Fonts/SFNSText-RegularG1.otf',
'/Library/Fonts/Microsoft/TaiLeb.ttf',
'/System/Library/Fonts/LastResort.ttf',
'/Library/Fonts/STIXSizTwoSymReg.otf',
'/Library/Fonts/WeibeiTC-Bold.otf',
'/Library/Fonts/STIXVarBol.otf',
'/Library/Fonts/Microsoft/Corbel Italic.ttf',
'/Library/Fonts/STIXSizTwoSymBol.otf',
'/System/Library/Fonts/SFNSText-LightItalic.otf',
'/System/Library/Fonts/SFNSText-RegularItalicG2.otf',
'/Library/Fonts/Trebuchet MS Bold Italic.ttf',
'/Library/Fonts/Microsoft/MingLiU_HKSCS-ExtB.ttf',
'/System/Library/Fonts/SFNSDisplay-Bold.otf',
'/System/Library/Fonts/SFNSText-RegularItalicG3.otf',
'/Library/Fonts/Microsoft/PMingLiU-ExtB.ttf',
'/Library/Fonts/Courier New Bold Italic.ttf',
'/Library/Fonts/Microsoft/Lucida Console.ttf',
'/Library/Fonts/STIXSizFourSymBol.otf',
'/Library/Fonts/STIXIntUpSmReg.otf',
'/Library/Fonts/Microsoft/Constantia Bold Italic.ttf',
'/Library/Fonts/华文黑体.ttf',
'/usr/X11/lib/X11/fonts/TTF/VeraBI.ttf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMNisibin.otf',
'/System/Library/Fonts/ZapfDingbats.ttf',
'/Library/Fonts/Microsoft/Cambria Math.ttf',
'/usr/X11/lib/X11/fonts/OTF/SyrCOMJerusalemOutline.otf',
'/usr/X11/lib/X11/fonts/TTF/VeraBd.ttf',
'/Library/Fonts/YuppyTC-Regular.otf']
In [34]:
# len(fonts) => 100以上はあるはず
# データフレームへの詰め込み
l = []
for f in fonts:
font = fm.FontProperties(fname=f)
l.append((f, font.get_name(), font.get_family()))
df = pd.DataFrame(l, columns=['path', 'name', 'family'])
# IPAフォントが存在することの確認
df[df['path'].apply(lambda s: 'IPA' in s)]
df
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-34-9d0af0bad071> in <module>()
4 for f in fonts:
5 font = fm.FontProperties(fname=f)
----> 6 l.append((f, font.get_name(), font.get_family()))
7 df = pd.DataFrame(l, columns=['path', 'name', 'family'])
8 # IPAフォントが存在することの確認
/Users/knt/.pyenv/versions/anaconda3-2.5.0/lib/python3.5/site-packages/matplotlib/font_manager.py in get_name(self)
735 properties.
736 """
--> 737 return ft2font.FT2Font(findfont(self)).family_name
738
739 def get_style(self):
RuntimeError: In FT2Font: Could not set the fontsize
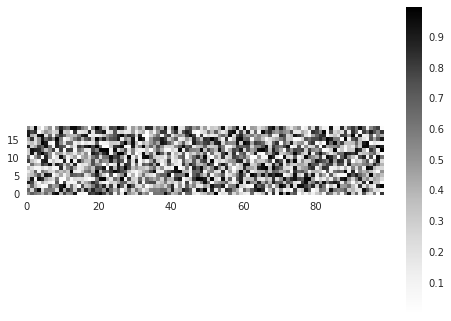
In [31]:
Nx = 100
Ny = 20
a = np.random.rand(Ny, Nx)
print(a.shape)
x = range(Nx)
y = range(Ny)
X, Y = np.meshgrid(x, y)
plt.pcolormesh(X, Y, a)
plt.axis("image")
plt.colorbar()
# plt.tight_layout()
#plt
(20, 100)
Out[31]:
<matplotlib.colorbar.Colorbar at 0x11aae3b70>
In [ ]:
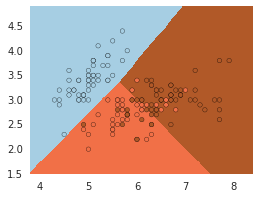
In [32]:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model, datasets
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, :2] # we only take the first two features.
Y = iris.target
h = .02 # step size in the mesh
# we create an instance of Neighbours Classifier and fit the data.
logreg = linear_model.LogisticRegression(C=1e5).fit(X, Y)
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, m_max]x[y_min, y_max].
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = logreg.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure(1, figsize=(4, 3))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=Y, edgecolors='k', cmap=plt.cm.Paired)
#plt.xlabel('Sepal length')
#plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
#plt.xticks(())
#plt.yticks(())
#plt.show()
Out[32]:
(1.5, 4.900000000000003)
In [ ]:
In [ ]:
name arguments
beta (a, b[, size])
binomial (n, p[, size])
chisquare (df[, size])
dirichlet (alpha[, size])
exponential ([scale, size])
beta¶
https://ja.wikipedia.org/wiki/%E3%83%99%E3%83%BC%E3%82%BF%E5%88%86%E5%B8%83
In [142]:
np.random.beta?
In [122]:
%%latex
$$
f(x; a,b) = \frac{1}{B(\alpha, \beta)} x^{\alpha - 1}
(1 - x)^{\beta - 1}
$$
$$
f(x; a,b) = \frac{1}{B(\alpha, \beta)} x^{\alpha - 1}
(1 - x)^{\beta - 1}
$$
ベータ関数¶
In [123]:
%%latex
$$
B(\alpha, \beta) = \int_0^1 t^{\alpha - 1}
(1 - t)^{\beta - 1} dt.
$$
$$
B(\alpha, \beta) = \int_0^1 t^{\alpha - 1}
(1 - t)^{\beta - 1} dt.
$$
In [171]:
np.random.beta(a=1, b=1, size=2)
Out[171]:
array([ 0.28408624, 0.47506511])
binomial¶
https://ja.wikipedia.org/wiki/%E4%BA%8C%E9%A0%85%E5%88%86%E5%B8%83
In [130]:
np.random.binomial?
In [128]:
%%latex
$$
P(N) = \binom{n}{N}p^N(1-p)^{n-N},
$$
$$
P(N) = \binom{n}{N}p^N(1-p)^{n-N},
$$
In [170]:
np.random.binomial(n=100, p=0.5, size=2)
Out[170]:
array([55, 49])
chisquare¶
https://ja.wikipedia.org/wiki/%E3%82%AB%E3%82%A4%E4%BA%8C%E4%B9%97%E5%88%86%E5%B8%83
In [162]:
np.random.chisquare?
In [166]:
%%latex
$$
Q = \sum_{i=0}^{\mathtt{df}} X^2_i
$$
$$
Q = \sum_{i=0}^{\mathtt{df}} X^2_i
$$
In [165]:
%%latex
$$
p(x) = \frac{(1/2)^{k/2}}{\Gamma(k/2)}
x^{k/2 - 1} e^{-x/2},
$$
$$
p(x) = \frac{(1/2)^{k/2}}{\Gamma(k/2)}
x^{k/2 - 1} e^{-x/2},
$$
ガンマ関数¶
In [164]:
%%latex
$$
\Gamma(x) = \int_0^{-\infty} t^{x - 1} e^{-t} dt.
$$
$$
\Gamma(x) = \int_0^{-\infty} t^{x - 1} e^{-t} dt.
$$
In [169]:
np.random.chisquare(df=2, size=2)
Out[169]:
array([ 3.11450218, 2.90912819])
dirichlet¶
https://ja.wikipedia.org/wiki/%E3%83%87%E3%82%A3%E3%83%AA%E3%82%AF%E3%83%AC%E5%88%86%E5%B8%83
In [172]:
np.random.dirichlet?
In [173]:
%%latex
$$
X \approx \prod_{i=1}^{k}{x^{\alpha_i-1}_i}
$$
$$
X \approx \prod_{i=1}^{k}{x^{\alpha_i-1}_i}
$$
In [174]:
%%latex
$$
X = \frac{1}{\sum_{i=1}^k{y_i}} (y_1, \ldots, y_n)
$$
$$
X = \frac{1}{\sum_{i=1}^k{y_i}} (y_1, \ldots, y_n)
$$
In [180]:
np.random.dirichlet(alpha=[1,1,1], size=2)
Out[180]:
array([[ 0.58039523, 0.18049816, 0.23910661],
[ 0.02770379, 0.64163565, 0.33066056]])
exponential¶
https://ja.wikipedia.org/wiki/%E6%8C%87%E6%95%B0%E5%88%86%E5%B8%83
In [181]:
np.random.exponential?
In [183]:
%%latex
$$
f(x; \frac{1}{\beta}) = \frac{1}{\beta} \exp(-\frac{x}{\beta})
$$
$$
f(x; \frac{1}{\beta}) = \frac{1}{\beta} \exp(-\frac{x}{\beta})
$$
In [192]:
%%latex
$$
\lambda = 1/\beta
$$
$$
\lambda = 1/\beta
$$
In [191]:
np.random.exponential(scale=1.0, size=2)
Out[191]:
array([ 0.38809756, 0.20912399])
In [ ]:
In [ ]:
## f
https://ja.wikipedia.org/wiki/F%E5%88%86%E5%B8%83
In [193]:
np.random.f?
# dfnum` (degrees of freedom in numerator)` and
# dfden` (degrees of freedom in denominator)`
In [ ]:
# expression not found
In [194]:
np.random.f(dfnum=2, dfden=3, size=2)
Out[194]:
array([ 4.5921271, 6.0671125])
In [ ]:
## gamma
https://ja.wikipedia.org/wiki/%E3%82%AC%E3%83%B3%E3%83%9E%E5%88%86%E5%B8%83
In [195]:
np.random.gamma?
In [196]:
%%latex
$$
p(x) = x^{k-1}\frac{e^{-x/\theta}}{\theta^k\Gamma(k)}
$$
$$
p(x) = x^{k-1}\frac{e^{-x/\theta}}{\theta^k\Gamma(k)}
$$
In [202]:
# first argument is shape
np.random.gamma(shape=1.0, scale=2.0, size=2)
Out[202]:
array([ 6.56908872, 1.78703692])
In [ ]:
## geometric
https://ja.wikipedia.org/wiki/%E5%B9%BE%E4%BD%95%E5%88%86%E5%B8%83
In [203]:
np.random.geometric?
In [204]:
%%latex
$$
f(k) = (1 - p)^{k - 1} p
$$
$$
f(k) = (1 - p)^{k - 1} p
$$
In [207]:
np.random.geometric(p=0.25, size=5)
Out[207]:
array([ 1, 10, 2, 1, 2])
gumbel¶
https://ja.wikipedia.org/wiki/%E3%82%AC%E3%83%B3%E3%83%99%E3%83%AB%E5%88%86%E5%B8%83
In [211]:
np.random.gumbel?
# scipy.stats.gumbel_l
# scipy.stats.gumbel_r
# scipy.stats.genextreme
# weibull
In [212]:
%%latex
$$
p(x) = \frac{e^{-(x - \mu)/ \beta}}{\beta} e^{ -e^{-(x - \mu)/
\beta}}
$$
$$
p(x) = \frac{e^{-(x - \mu)/ \beta}}{\beta} e^{ -e^{-(x - \mu)/
\beta}}
$$
In [209]:
np.random.gumbel(loc=0.0, scale=1.0, size=5)
Out[209]:
array([ 1.52374816, 1.21909239, -0.34864738, 1.30255025, -0.18242571])
hypergeometric¶
https://ja.wikipedia.org/wiki/%E8%B6%85%E5%B9%BE%E4%BD%95%E5%88%86%E5%B8%83
In [215]:
np.random.hypergeometric?
In [253]:
%%latex
$$
P(x) = \frac{\binom{m}{n}\binom{N-m}{n-x}}{\binom{N}{n}}
$$
$$
P(x) = \frac{\binom{m}{n}\binom{N-m}{n-x}}{\binom{N}{n}}
$$
In [241]:
%%latex
$$
0 \le x \le m
,
n+m-N \le x \le n
$$
$$
0 \le x \le m
,
n+m-N \le x \le n
$$
In [252]:
np.random.hypergeometric(ngood=150, nbad=50, nsample=100, size=5)
Out[252]:
array([78, 78, 77, 76, 76])
In [ ]:
## laplace
https://ja.wikipedia.org/wiki/%E3%83%A9%E3%83%97%E3%83%A9%E3%82%B9%E5%88%86%E5%B8%83
In [254]:
np.random.laplace?
In [256]:
%%latex
$$
f(x; \mu, \lambda) = \frac{1}{2\lambda}
\exp\left(-\frac{|x - \mu|}{\lambda}\right)
$$
$$
f(x; \mu, \lambda) = \frac{1}{2\lambda}
\exp\left(-\frac{|x - \mu|}{\lambda}\right)
$$
In [257]:
np.random.laplace(loc=0.0, scale=1.0, size=5)
Out[257]:
array([ 0.08519469, -0.14605399, 0.45948552, 0.58416639, -0.5740138 ])
logistic¶
In [258]:
np.random.logistic?
In [260]:
%%latex
$$
P(x) = P(x) = \frac{e^{-(x-\mu)/s}}{s(1+e^{-(x-\mu)/s})^2}
$$
$$
P(x) = P(x) = \frac{e^{-(x-\mu)/s}}{s(1+e^{-(x-\mu)/s})^2}
$$
In [261]:
np.random.logistic(loc=0, scale=1, size=5)
Out[261]:
array([ 1.73006169, 0.07923837, 1.69364654, 2.61801514, -0.00910529])
lognormal¶
https://ja.wikipedia.org/wiki/%E5%AF%BE%E6%95%B0%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83
In [262]:
np.random.lognormal?
In [263]:
%%latex
$$
p(x) = \frac{1}{\sigma x \sqrt{2\pi}}
e^{(-\frac{(ln(x)-\mu)^2}{2\sigma^2})}
$$
$$
p(x) = \frac{1}{\sigma x \sqrt{2\pi}}
e^{(-\frac{(ln(x)-\mu)^2}{2\sigma^2})}
$$
In [264]:
np.random.lognormal(mean=0, sigma=1, size=5)
Out[264]:
array([ 0.60342456, 1.32460941, 4.77135422, 0.1564132 , 0.25944637])
logseries¶
In [277]:
np.random.logseries?
In [278]:
%%latex
$$
P(k) = \frac{-p^k}{k \ln(1-p)}
$$
$$
P(k) = \frac{-p^k}{k \ln(1-p)}
$$
In [279]:
np.random.logseries(p=0.5, size=5)
Out[279]:
array([1, 1, 3, 1, 2])
multinomial¶
https://ja.wikipedia.org/wiki/%E5%A4%9A%E9%A0%85%E5%88%86%E5%B8%83
In [280]:
np.random.multinomial?
In [283]:
%%latex
$$
f(x_1,\ldots,x_k;n,p_1,\ldots,p_k) =
\begin
{cases}
{n! \over x_1!\cdots x_k!}p_1^{x_1}\cdots p_k^{x_k} \quad &
\mbox{when } \sum_{i=1}^k x_i=n
\\
0 &
\mbox{otherwise.}
\end
{cases}
$$
$$
f(x_1,\ldots,x_k;n,p_1,\ldots,p_k) =
\begin
{cases}
{n! \over x_1!\cdots x_k!}p_1^{x_1}\cdots p_k^{x_k} \quad &
\mbox{when } \sum_{i=1}^k x_i=n
\\
0 &
\mbox{otherwise.}
\end
{cases}
$$
In [ ]:
np.random.multinomial(n=, pvals=, size=5)
multivariate_normal¶
- https://en.wikipedia.org/wiki/Multivariate_normal_distribution
- https://ja.wikipedia.org/wiki/%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83#.E5.A4.9A.E5.A4.89.E9.87.8F.E6.AD.A3.E8.A6.8F.E5.88.86.E5.B8.83
In [284]:
np.random.multivariate_normal?
In [304]:
%%latex
$$
???
$$
$$
???
$$
In [303]:
np.random.multivariate_normal(mean=[0, 1], cov=[[1, 0], [0, 1]], size=5)
Out[303]:
array([[-0.47681492, 0.66149071],
[ 0.02377642, 2.54830277],
[-0.95989893, 1.90386633],
[-0.94160488, -0.84989032],
[-0.06047647, 0.29223881]])
negative_binomial¶
https://ja.wikipedia.org/wiki/%E8%B2%A0%E3%81%AE%E4%BA%8C%E9%A0%85%E5%88%86%E5%B8%83
In [305]:
np.random.negative_binomial?
In [306]:
%%latex
$$
P(N;n,p) = \binom{N+n-1}{n-1}p^{n}(1-p)^{N}
$$
$$
P(N;n,p) = \binom{N+n-1}{n-1}p^{n}(1-p)^{N}
$$
In [315]:
np.random.negative_binomial(n=3, p=0.5, size=5)
Out[315]:
array([4, 8, 4, 0, 6])
noncentral_chisquare¶
- https://ja.wikipedia.org/wiki/%E9%9D%9E%E5%BF%83%E3%82%AB%E3%82%A4%E4%BA%8C%E4%B9%97%E5%88%86%E5%B8%83
- 非心
- https://en.wikipedia.org/wiki/Noncentral_chi-squared_distribution
In [316]:
np.random.noncentral_chisquare?
In [320]:
%%latex
$$
P(x;df,nonc) = \sum^{\infty}_{i=0}
\frac{e^{-nonc/2}(nonc/2)^{i}}{i!}
\P_{Y_{df+2i}}(x)
$$
$$
P(x;df,nonc) = \sum^{\infty}_{i=0}
\frac{e^{-nonc/2}(nonc/2)^{i}}{i!}
\P_{Y_{df+2i}}(x)
$$
In [321]:
np.random.noncentral_chisquare(df=2, nonc=1, size=5)
Out[321]:
array([ 0.7826903 , 0.39724018, 2.10628494, 3.15303285, 1.77351514])
noncentral_f¶
In [322]:
np.random.noncentral_f?
In [324]:
%%latex
$$
???
$$
$$
???
$$
In [323]:
np.random.noncentral_f(dfnum=2, dfden=2, nonc=1, size=5)
Out[323]:
array([ 1.19224776, 3.47312157, 5.24914716, 0.18250845, 0.74879712])
normal¶
https://ja.wikipedia.org/wiki/%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83
In [325]:
np.random.normal?
In [327]:
%%latex
$$
p(x) = \frac{1}{\sqrt{ 2 \pi \sigma^2 }}
e^{ - \frac{ (x - \mu)^2 } {2 \sigma^2} }
$$
$$
p(x) = \frac{1}{\sqrt{ 2 \pi \sigma^2 }}
e^{ - \frac{ (x - \mu)^2 } {2 \sigma^2} }
$$
In [326]:
np.random.normal(loc=0.0, scale=1.0, size=5)
Out[326]:
array([ 1.72200361, 1.91580832, 0.15465406, 1.56988389, 1.42359534])
pareto¶
https://ja.wikipedia.org/wiki/%E3%83%91%E3%83%AC%E3%83%BC%E3%83%88%E5%88%86%E5%B8%83
In [329]:
np.random.pareto?
In [330]:
%%latex
$$
p(x) = \frac{am^a}{x^{a+1}}
$$
$$
p(x) = \frac{am^a}{x^{a+1}}
$$
In [ ]:
np.random.pareto(a=, size=5)
poisson¶
https://ja.wikipedia.org/wiki/%E3%83%9D%E3%82%A2%E3%82%BD%E3%83%B3%E5%88%86%E5%B8%83
In [331]:
np.random.poisson?
In [357]:
%%latex
$$
f(k; \lambda)=\frac{\lambda^k e^{-\lambda}}{k!}
$$
$$
f(k; \lambda)=\frac{\lambda^k e^{-\lambda}}{k!}
$$
In [356]:
np.random.poisson(lam=2, size=10)
Out[356]:
array([1, 2, 2, 1, 2, 0, 3, 3, 2, 0])
power¶
？？
In [358]:
np.random.power?
In [360]:
%%latex
$$
P(x; a) = ax^{a-1}, 0 \le x \le 1, a>0
$$
$$
P(x; a) = ax^{a-1}, 0 \le x \le 1, a>0
$$
In [359]:
np.random.power(a=0.5, size=5)
Out[359]:
array([ 0.50392877, 0.04684049, 0.00144087, 0.37744684, 0.27361199])
rayleigh¶
https://ja.wikipedia.org/wiki/%E3%83%AC%E3%82%A4%E3%83%AA%E3%83%BC%E5%88%86%E5%B8%83
In [364]:
np.random.rayleigh?
In [366]:
%%latex
$$
P(x;scale) = \frac{x}{scale^2}e^{\frac{-x^2}{2 \cdotp scale^2}}
$$
$$
P(x;scale) = \frac{x}{scale^2}e^{\frac{-x^2}{2 \cdotp scale^2}}
$$
In [365]:
np.random.rayleigh(scale=1.0, size=5)
Out[365]:
array([ 2.70600975, 0.46129338, 1.05866746, 1.1758816 , 0.66072779])
In [378]:
plt.hist?
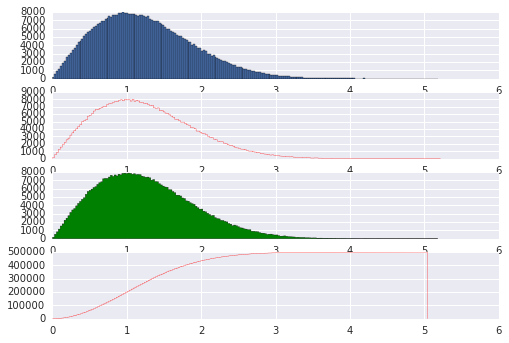
In [382]:
fig, axes = plt.subplots(4)
axes[0].hist(np.random.rayleigh(scale=1.0, size=500000), bins=200)
axes[1].hist(np.random.rayleigh(scale=1.0, size=500000), bins=200, histtype="step", color="red")
axes[2].hist(np.random.rayleigh(scale=1.0, size=500000), bins=200, histtype="stepfilled", color="green")
axes[3].hist(np.random.rayleigh(scale=1.0, size=500000), bins=200, histtype="step", color="red", cumulative=True)
""
Out[382]:
''
In [414]:
rayleigh.ppf(0.01), rayleigh.ppf(0.99), x
Out[414]:
(0.14177683769573535,
3.0348542587702925,
array([ 0.14177684, 0.17099984, 0.20022285, 0.22944585, 0.25866885,
0.28789186, 0.31711486, 0.34633787, 0.37556087, 0.40478388,
0.43400688, 0.46322988, 0.49245289, 0.52167589, 0.5508989 ,
0.5801219 , 0.60934491, 0.63856791, 0.66779091, 0.69701392,
0.72623692, 0.75545993, 0.78468293, 0.81390594, 0.84312894,
0.87235194, 0.90157495, 0.93079795, 0.96002096, 0.98924396,
1.01846697, 1.04768997, 1.07691297, 1.10613598, 1.13535898,
1.16458199, 1.19380499, 1.223028 , 1.252251 , 1.281474 ,
1.31069701, 1.33992001, 1.36914302, 1.39836602, 1.42758902,
1.45681203, 1.48603503, 1.51525804, 1.54448104, 1.57370405,
1.60292705, 1.63215005, 1.66137306, 1.69059606, 1.71981907,
1.74904207, 1.77826508, 1.80748808, 1.83671108, 1.86593409,
1.89515709, 1.9243801 , 1.9536031 , 1.98282611, 2.01204911,
2.04127211, 2.07049512, 2.09971812, 2.12894113, 2.15816413,
2.18738714, 2.21661014, 2.24583314, 2.27505615, 2.30427915,
2.33350216, 2.36272516, 2.39194817, 2.42117117, 2.45039417,
2.47961718, 2.50884018, 2.53806319, 2.56728619, 2.59650919,
2.6257322 , 2.6549552 , 2.68417821, 2.71340121, 2.74262422,
2.77184722, 2.80107022, 2.83029323, 2.85951623, 2.88873924,
2.91796224, 2.94718525, 2.97640825, 3.00563125, 3.03485426]))
- http://docs.scipy.org/doc/scipy-0.17.0/reference/generated/scipy.stats.norm.html
- http://docs.scipy.org/doc/scipy-0.17.0/reference/generated/scipy.stats.rv_continuous.html
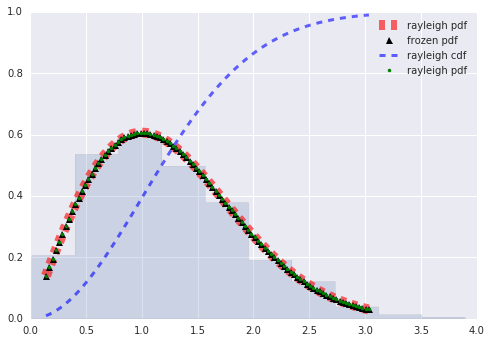
In [423]:
from scipy.stats import rayleigh
fig, ax = plt.subplots(1, 1)
# Alternatively, the distribution object can be called (as a function) to fix the shape, location and scale parameters.
# This returns a “frozen” RV object holding the given parameters fixed.
# Freeze the distribution and display the frozen pdf:
rv = rayleigh()
mean, var, skew, kurt = rayleigh.stats(moments='mvsk')
x = np.linspace(rayleigh.ppf(0.01), rayleigh.ppf(0.99), 100)
ax.plot(x, rayleigh.pdf(x), 'r--', lw=10, alpha=0.6, label='rayleigh pdf')
ax.plot(x, rv.pdf(x), 'k^', lw=6, label='frozen pdf')
ax.plot(x, rayleigh.cdf(x), 'b--', lw=3, alpha=0.6, label='rayleigh cdf')
ax.plot(x, rayleigh.pdf(x), 'g.', lw=2, label='rayleigh pdf')
# Check accuracy of cdf and ppf:
vals = rayleigh.ppf([0.001, 0.5, 0.999])
np.allclose([0.001, 0.5, 0.999], rayleigh.cdf(vals))
# True
# Generate random numbers: And compare the histogram:
r = rayleigh.rvs(size=1000)
n, bins, patches = ax.hist(r, normed=True, histtype='stepfilled', alpha=0.2)
ax.legend(loc='best', frameon=False)
n, bins, patches
Out[423]:
(array([ 0.20597831, 0.53554361, 0.58961291, 0.49692268, 0.37848515,
0.19052994, 0.12101226, 0.03862093, 0.01287364, 0.00514946]),
array([ 0.0145884 , 0.40297881, 0.79136921, 1.17975962, 1.56815003,
1.95654043, 2.34493084, 2.73332125, 3.12171165, 3.51010206,
3.89849247]),
<a list of 1 Patch objects>)
standard_cauchy¶
In [424]:
np.random.standard_cauchy?
In [426]:
%%latex
$$
P(x; x_0, \gamma) = \frac{1}{\pi \gamma \bigl[ 1+
(\frac{x-x_0}{\gamma})^2 \bigr] }
$$
$$
P(x; x_0, \gamma) = \frac{1}{\pi \gamma \bigl[ 1+
(\frac{x-x_0}{\gamma})^2 \bigr] }
$$
In [425]:
np.random.standard_cauchy(size=5)
Out[425]:
array([-2.40019962, -0.4644643 , 0.52742126, -0.45076806, 2.80696267])
standard_exponential¶
https://ja.wikipedia.org/wiki/%E6%8C%87%E6%95%B0%E5%88%86%E5%B8%83
In [427]:
np.random.standard_exponential?
standard_exponential is identical to the exponential distribution
with a scale parameter of 1.
In [428]:
np.random.standard_exponential(size=5)
Out[428]:
array([ 0.60078119, 0.3681998 , 3.48541253, 1.60442092, 0.37735774])
standard_gamma¶
https://en.wikipedia.org/wiki/Generalized_gamma_distribution ?
In [431]:
np.random.standard_gamma?
In [432]:
%%latex
$$
p(x) = x^{k-1}\frac{e^{-x/\theta}}{\theta^k\Gamma(k)}
$$
$$
p(x) = x^{k-1}\frac{e^{-x/\theta}}{\theta^k\Gamma(k)}
$$
In [433]:
# scale = 1 ?
np.random.standard_gamma(shape=7.5, size=5)
Out[433]:
array([ 10.04271151, 12.83452788, 6.77340362, 3.43550584, 5.81463822])
standard_normal¶
In [434]:
np.random.standard_normal?
In [435]:
# Draw samples from a standard Normal distribution (mean=0, stdev=1).
np.random.standard_normal(size=5)
Out[435]:
array([-0.2389675 , 0.99376433, 0.23754419, 0.17881443, 0.31359466])
standard_t¶
https://ja.wikipedia.org/wiki/T%E5%88%86%E5%B8%83
In [436]:
np.random.standard_t?
In [437]:
%%latex
$$
P(x, df) = \frac{\Gamma(\frac{df+1}{2})}{\sqrt{\pi df}
\Gamma(\frac{df}{2})}\Bigl( 1+\frac{x^2}{df} \Bigr)^{-(df+1)/2}
$$
$$
P(x, df) = \frac{\Gamma(\frac{df+1}{2})}{\sqrt{\pi df}
\Gamma(\frac{df}{2})}\Bigl( 1+\frac{x^2}{df} \Bigr)^{-(df+1)/2}
$$
In [438]:
np.random.standard_t(df=2, size=5)
Out[438]:
array([ 0.85404676, 2.16559892, -2.68894434, 2.27305289, -1.57081979])
triangular¶
- https://ja.wikipedia.org/wiki/%E4%B8%89%E8%A7%92%E5%88%86%E5%B8%83
- https://en.wikipedia.org/wiki/Triangular_distribution
In [439]:
np.random.triangular?
In [441]:
%%latex
$$
P(x;l, m, r) =
\begin{cases}
\frac{2(x-l)}{(r-l)(m-l)} & \text{for $l \leq x \leq m$},\\
\frac{2(m-x)}{(r-l)(r-m)} & \text{for $m \leq x \leq r$},\\
0 & \text{otherwise}.
\end{cases}
$$
$$
P(x;l, m, r) =
\begin{cases}
\frac{2(x-l)}{(r-l)(m-l)} & \text{for $l \leq x \leq m$},\\
\frac{2(m-x)}{(r-l)(r-m)} & \text{for $m \leq x \leq r$},\\
0 & \text{otherwise}.
\end{cases}
$$
In [443]:
# `left <= mode <= right`
np.random.triangular(left=2, mode=3, right=5, size=5)
Out[443]:
array([ 3.49152131, 3.0465073 , 2.97680472, 4.01562676, 4.2223051 ])
uniform¶
- https://ja.wikipedia.org/wiki/%E9%80%A3%E7%B6%9A%E4%B8%80%E6%A7%98%E5%88%86%E5%B8%83
- https://ja.wikipedia.org/wiki/%E9%9B%A2%E6%95%A3%E4%B8%80%E6%A7%98%E5%88%86%E5%B8%83
In [445]:
np.random.uniform?
In [447]:
%%latex
$$
p(x) = \frac{1}{b - a}
$$
$$
p(x) = \frac{1}{b - a}
$$
In [446]:
np.random.uniform(low=0.0, high=2.0, size=5)
Out[446]:
array([ 0.46382253, 0.98243351, 0.71326653, 0.9396711 , 1.96862686])
vonmises¶
- https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A9%E3%83%B3%E3%83%BB%E3%83%9F%E3%83%BC%E3%82%BC%E3%82%B9%E5%88%86%E5%B8%83
- フォン・ミーゼス
- https://en.wikipedia.org/wiki/Von_Mises_distribution
In [450]:
np.random.vonmises?
In [449]:
%%latex
$$
p(x) = \frac{e^{\kappa cos(x-\mu)}}{2\pi I_0(\kappa)}
$$
$$
p(x) = \frac{e^{\kappa cos(x-\mu)}}{2\pi I_0(\kappa)}
$$
In [ ]:
# mu: Mode ("center") of the distribution.
np.random.vonmises(mu=, kappa=, size=5)
wald¶
- https://ja.wikipedia.org/wiki/%E9%80%86%E3%82%AC%E3%82%A6%E3%82%B9%E5%88%86%E5%B8%83
- ワルド(逆ガウス)分布
- https://en.wikipedia.org/wiki/Inverse_Gaussian_distribution
In [451]:
np.random.wald?
In [452]:
%%latex
$$
P(x;mean,scale) = \sqrt{\frac{scale}{2\pi x^3}}e^
\frac{-scale(x-mean)^2}{2\cdotp mean^2x}
$$
$$
P(x;mean,scale) = \sqrt{\frac{scale}{2\pi x^3}}e^
\frac{-scale(x-mean)^2}{2\cdotp mean^2x}
$$
In [454]:
np.random.wald(mean=1, scale=1, size=5)
Out[454]:
array([ 0.57783556, 0.79730746, 0.56055645, 4.75489764, 0.73628504])
weibull¶
- https://ja.wikipedia.org/wiki/%E3%83%AF%E3%82%A4%E3%83%96%E3%83%AB%E5%88%86%E5%B8%83
- https://en.wikipedia.org/wiki/Weibull_distribution
- のrelated distribution ?
In [455]:
np.random.weibull?
In [457]:
%%latex
$$
p(x) = \frac{a}
{\lambda}(\frac{x}{\lambda})^{a-1}e^{-(x/\lambda)^a},
$$
$$
p(x) = \frac{a}
{\lambda}(\frac{x}{\lambda})^{a-1}e^{-(x/\lambda)^a},
$$
In [456]:
%%latex
$$
X = (-ln(U))^{1/a}
$$
$$
X = (-ln(U))^{1/a}
$$
In [458]:
np.random.weibull(a=1, size=5)
Out[458]:
array([ 0.58002483, 0.6534011 , 0.09482982, 0.54980911, 1.50052021])
zipf¶
- https://ja.wikipedia.org/wiki/%E3%82%B8%E3%83%83%E3%83%97%E3%81%AE%E6%B3%95%E5%89%87
- https://en.wikipedia.org/wiki/Zipf%27s_law
In [459]:
np.random.zipf?
In [460]:
%%latex
$$
p(x) = \frac{x^{-a}}{\zeta(a)},
$$
$$
p(x) = \frac{x^{-a}}{\zeta(a)},
$$
In [462]:
np.random.zipf(a=2, size=5)
Out[462]:
array([1, 2, 5, 1, 1])
In [ ]:
name arguments
beta (a, b[, size])
binomial (n, p[, size])
chisquare (df[, size])
dirichlet (alpha[, size])
exponential ([scale, size])
f (dfnum, dfden[, size])
gamma (shape[, scale, size])
geometric (p[, size])
gumbel ([loc, scale, size])
hypergeometric (ngood, nbad, nsample[, size])
laplace ([loc, scale, size])
logistic ([loc, scale, size])
lognormal ([mean, sigma, size])
logseries (p[, size])
multinomial (n, pvals[, size])
multivariate_normal (mean, cov[, size])
negative_binomial (n, p[, size])
noncentral_chisquare (df, nonc[, size])
noncentral_f (dfnum, dfden, nonc[, size])
normal ([loc, scale, size])
pareto (a[, size])
poisson ([lam, size])
power (a[, size])
rayleigh ([scale, size])
standard_cauchy ([size])
standard_exponential ([size])
standard_gamma (shape[, size])
standard_normal ([size])
standard_t (df[, size])
triangular (left, mode, right[, size])
uniform ([low, high, size])
vonmises (mu, kappa[, size])
wald (mean, scale[, size])
weibull (a[, size])
zipf (a[, size])
In [ ]:
In [ ]:
In [ ]:
In [ ]: